Complex mexican hat wavelet
The complex Mexican hat wavelet is a low-oscillation, complex-valued, wavelet for the continuous wavelet transform. This wavelet is formulated in terms of its Fourier transform as the Hilbert analytic function of the conventional Mexican hat wavelet:
Temporally, this wavelet can be expressed in terms of the error function, as:
This wavelet has 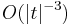 asymptotic temporal decay in
asymptotic temporal decay in 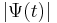 , dominated by the discontinuity of the second derivative of
, dominated by the discontinuity of the second derivative of 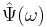 at
at 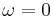 .
.
This wavelet was proposed in 2002 by Addison et al. for applications requiring high temporal precision time-frequency analysis.
References
1. Paul S. Addison Wavelet Page - Low-Oscillation Complex Wavelets, P. S. Addison, et al., The Journal of Sound and Vibration, 2002
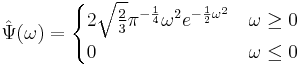
![\Psi(t)=\frac{2}{\sqrt{3}}\pi^{-\frac{1}{4}}\left(\sqrt{\pi}(1-t^{2})e^{-\frac{1}{2}t^{2}}-\left(\sqrt{2}it%2B\sqrt{\pi}\textrm{erf}\left[\frac{i}{\sqrt{2}}t\right]\left(1-t^{2}\right)e^{-\frac{1}{2}t^{2}}\right)\right)](/2012-wikipedia_en_all_nopic_01_2012/I/9c83c16664929012d9a5bfdae9e4024b.png)